1.กราฟ
ทฤษฎีกราฟ
ด้วยแผนภาพที่ประกอบด้วยจุด และเส้นที่เชื่อมระหว่างจุด 2 จุด• ตัวอย่างเช่น
- แผนภาพที่แสดงเส้นทางของรถไฟฟ้า BTS
- แผนภาพที่แสดงถนนที่เชื่อมเมืองต่าง ๆ
- แผนภาพแสดงโครงสร้างทางเคมีของสารประกอบ
ไฮโดรคาร์บอน
- วงจรไฟฟ้า
- แผนภาพเครือข่ายคอมพิวเตอร์
- แผนภาพแสดงเส้นทางการบิน
บทนิยาม กราฟ G ประกอบด้วย เซตจำกัด 2 เซต คือ 1. เซตที่ไม่เป็นเซตว่างของจุดยอด (Vertex) แทนด้วยสัญลักษณ์ V(G) 2. เซตของเส้นเชื่อม (Edge) ที่เชื่อมระหว่างจุด ยอด แทนด้วยสัญลักษณ์ E(G) |
ข้อสังเกต V(G) ≠ ∅ แต่ E(G) อาจเป็นเซตว่างได้
บทนิยาม จุดยอด u และจุดยอด v ของกราฟ เป็นจุดยอดประชิด (Adjacent Vertices) ก็ต่อเมื่อ มีเส้นเชื่อมระหว่างจุดทั้งสอง และเราเรียกจุดยอด u และ v ว่าจุดปลาย (End Point) ของเส้นเชื่อมนั้น
เส้นเชื่อม e ของกราฟ เกิดกับ (Incident) จุดยอด v ถ้าจุดยอด v เป็นจุดปลายจุดหนึ่งของเส้นเชื่อม |

จากกราฟของตัวอย่างที่ 1 จะเห็นว่า
จุดยอด A และจุดยอด B เป็นจุดยอดประชิด
จุดยอด A และจุดยอด C เป็นจุดยอดประชิด
จุดยอด B และจุดยอด C เป็นจุดยอดประชิด
จุดยอด C และจุดยอด D เป็นจุดยอดประชิด
แต่ จุดยอด A และจุดยอด D ไม่เป็นจุดยอดประชิด
จุดยอด B และจุดยอด D ไม่เป็นจุดยอดประชิด
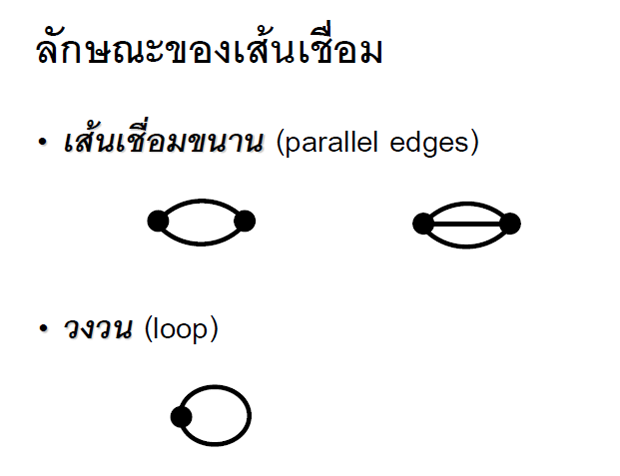
บทนิยาม เส้นเชื่อมตั้งแต่ 2 เส้นที่เชื่อมระหว่างจุดยอดคู่เดียวกัน เรียกว่า เส้นเชื่อมขนาน(Parallel Edges) เส้นเชื่อมที่เชื่อมจุดยอดเพียงจุดเดียว เรียกว่า วงวน
(Loop)
|

จากรูปข้างต้นจะเห็นว่า
e1 และ e2 เป็น เส้นเชื่อมขนาน เส้นเชื่อม e5 เป็นวงวน ในกรณีที่กราฟไม่มีเส้นเชื่อมขนาน สามารถใช้สัญลักษณ์
AB เพื่อแทนเส้นเชื่อมระหว่างจุดยอด A และ B ได้ เช่น กราฟในตัวอย่างที่ 1 สามารถเขียนเซตของเส้นเชื่อม E(G)
ได้ใหม่เป็น E(G) = {AB, BC, AC, CD}
2.ดีกรีของจุดยอด
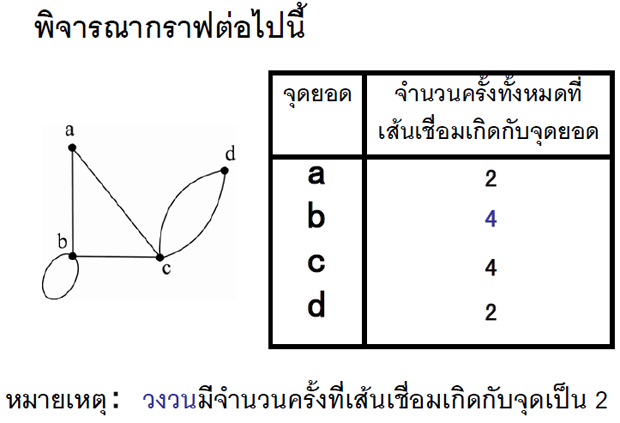
บทนิยาม ดีกรี (Degree) ของจุดยอด v ในกราฟ คือ จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด v
ใช้สัญลักษณ์ deg v แทนดีกรีของจุดยอด |
จะเห็นว่า เส้นเชื่อมที่เกิดกับจุดยอด a ได้แก่ เส้นเชื่อม ab และ ac ดังนั้น จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด a
คือ 2 สำหรับจุดยอด b มีเส้นเชื่อมที่เกิดกับจุดยอด b ได้แก่ เส้นเชื่อม ba, bc และ bb เป็นวงวน เกิดกับจุดยอด b
กรณีที่มีเส้นเชื่อมเป็นวงวน จะกำหนดให้นับจำนวนเส้นเชื่อมที่เกิดกับจุดยอดนั้นเพิ่มขึ้น โดยให้นับเส้นเชื่อมที่เป็นวงวน 1 วง วงวนเป็น 2 ดังนั้นจำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด b จึงเป็น 4
ทฤษฎีบท 1
ผลรวมของดีกรีของจุดยอดทุดจุดในกราฟเท่ากับสองเท่าของจำนวนเส้นเชื่อมในกราฟ
|
เนื่องจากเส้นเชื่อมแต่ละเส้นในกราฟเกิดกับจุดยอดเป็นจำนวน 2 ครั้ง ดังนั้นเส้นเชื่อมแต่ละเส้นจะถูกนับ 2 ครั้งในผลรวมของดีกรีของจุดยอดทุกจุด
นั่นคือ ผลรวมของดีกรีของจุดยอดทุกจุดในกราฟเท่ากับสองเท่าของจำนวนเส้นเชื่อมในกราฟ
บทนิยาม
จุดยอดที่มีดีกรีเป็นจำนวนคู่ เรียกว่า จุดยอดคู่ (Even Vertex)
จุดยอดที่มีดีกรีเป็นจำนวนคี่ เรียกว่า จุดยอดคี่ (Odd Vertex)
|
ทฤษฎีบท 2 ทุกกราฟจะมีจุดยอดคี่เป็นจำนวนคู่
|
3.แนวเดินและกราฟเชื่อมโยง
บทนิยาม ให้ u และ v เป็นจุดยอดของกราฟแนวเดิน
u - v (u - v walk) คือ ลำดับจำกัดของจุดยอดและเส้นเชื่อมสลับกัน
u = u0, e1, u1, e2, u2, …, un-1, en, un = v
โดยเริ่มต้นที่จุดยอด u และสิ้นสุดที่จุดยอด v และแต่ละเส้นเชื่อม ei จะเกิดกับจุดยอดui-1 และ ui เมื่อ i ∈ {1, 2, …, n}
|
บทนิยาม
รอยเดิน (trail) คือ แนวเดินในกราฟที่เส้นเชื่อมทั้งหมดแตกต่างกัน
วิถี(Path) คือ แนวเดินในกราฟที่จุดยอดทั้งหมดแตกต่างกัน วงจร(Circuit) คือ แนวเดินที่เส้นเชื่อมทั้งหมดแตกต่างกัน โดยมีจุดเริ่มต้นและจุดสุดท้ายเป็นจุดยอดเดียวกัน วัฏจักร(Cycle) คือวงจรที่ไม่มีจุดยอดซ้ำกัน ยกเว้นจุดเริ่มต้นและจุดสุดท้าย
|
บทนิยาม กราฟ G เป็นกราฟเชื่อมโยง(connected graph) ถ้าจุดยอด 2 จุดใดๆ ใน G เชื่อได้ด้วยวิถี
|
4.กราฟถ่วงน้ำหนัก
บทนิยาม
ค่าน้ำหนัก(weight) ของเส้นเชื่อม e ในกราฟ คือ จำนวนที่ไม่เป็นลบที่กำหนดไว้บนเส้นเชื่อม e
กราฟถ่วงน้ำหนัก(weight graph) คือ กราฟที่เส้นเชื่อมทุกเส้นมีค่าน้ำหนัก
|
บทนิยาม วิถีที่สั้นที่สุด จากจุด A ถึงจุดยอด Z ในกราฟถ่วงน้ำหนัก คือวิถี A - Z ที่ผลรวมของค่าน้ำหนักของเส้นเชื่อมทุกเส้นในวิถี A-Z น้อยที่สุด
|
5. กราฟออยเลอร์
ทฤษฎีบทต่อไปนี้ ให้เงื่อนไขว่า กราฟที่กำหนดให้เป็นกราฟออยเลอร์เมื่อไร
ทฤษฎีบทต่อไปนี้ ให้เงื่อนไขว่า กราฟที่กำหนดให้มีรอยเดินออยเลอร์เมื่อไร
ลักษณะเฉพาะของต้นไม้
ทฤษฎีบท 1. ให้ T เป็นกราฟที่ไม่มีวงวน กราฟ T เป็นต้นไม้ ก็ต่อเมื่อ จุดยอด 2 จุดใดๆ ใน T เชื่อมโยงกันได้ด้วยวิถีเพียงวิถีเดียว 2. ให้ T เป็นกราฟที่มีจำนวนจุดยอดเป็น n จุด กราฟ T เป็นต้นไม้ ก็ต่อเมื่อ กราฟ T ไม่มีวัฏจักร และมีเส้นเชื่อม n – 1 เส้น 3. ให้ T เป็นกราฟที่มีจำนวนจุดยอดเป็น n จุด กราฟ T เป็นต้นไม้ ก็ต่อเมื่อ กราฟ T เป็นกราฟเชื่อมโยงและมีเส้นเชื่อม n – 1 เส้น 4. ถ้า T เป็นต้นไม้ที่มีจำนวนจุดยอดอย่างน้อย 2 จุด แล้ว กราฟ T จะมีดีกรี 1 อย่างน้อย 2 จุด
ต้นไม้แผ่ทั่ว (spanning tree)
ก่อนที่จะศึกษาต้นไม้แผ่ทั่ว เราจะเริ่มต้นศึกษากราฟย่อยก่อน
แบบทดสอบ

1)จากกราฟมีจุดยอดคู่กี่จุด
1. 2
2. 3
3. 4
4. 5
2)จากกราฟมีจุดยอดคี่กี่จุด
1. 2
2. 3
3. 4
4. 5
3)วิถีที่สั้นที่สุดของกราฟนี้
1. D-A-B-C-E-F
2. A-B-C-E-F-D
3. B-A-E-F-D-C
4. F-E-C-A-D-B
4) ผลรวมของดีกรีของกราฟมีค่าเท่าไร
1. 15
2.16
3.17
4.18
5) กราฟนี้มีค่าน้ำหนักเท่าไร
1. 20
2. 23
3. 26
4. 28
เฉลย
1) 3 2) 1 3) 1 4) 4 5) 4
|